22-5-2011 | KHOA HỌC

Giải Bài Tập Hình Học từ 11 đến 20

  T. V. PHÊ & NGUYỄN TIN

11  12  13  14  15  16  17  18  19  20

:: Bài 11

Cho tam giác cân ABC. Chọn điểm D trên BC sao cho BD = 2DC. Chọn điểm P trên AD sao cho BPD = BAC. Chứng Minh:  BAC = 2 DPC

BÀI GIẢI

a) S(BPD) = (BD . h0) / 2

S(DPC) = (DC . h0) / 2

Vì BD = 2 DC nên S(BPD) = 2 S(DPC)

S(BPD) = (PD . h2) / 2

S(DPC) = (PD . h1) / 2

Vì S(BPD) = 2 S(DPC) nên h2 = 2 h1

S(ABP) = (AP . h2) / 2

S(APC) = (AP . h1) / 2

Vì h2 = 2h1 nên S(ABP) = 2 S(APC) 

Trong ABP, ta có BPD = B1 + A2 (góc ngoài bằng hai góc trong không kề với nó), mà  A  = A1 + A2 và theo giả thiết BPD = A, vậy B1 = A1

Nếu chọn điểm I trên BP sao cho BI = AP ta sẽ có hai tam giác ABI và APC bằng nhau (BI=AP, AB=AC, B1 = A1). Vậy S(ABP) = 2S(APC) = 2S(ABI)

S(ABP) = (BP. h) / 2

S(ABI) = (BI . h) / 2

Vì S(ABP) = 2 S(ABI) nên BP = 2 BI, do đó BP = 2 AP

b) Hai tam giác bằng nhau ABI và APC cũng cho BAI = C2.

Góc ngoài BPD của tam giác cân AIP ==> BPD = 2I1.

Góc ngoài I1 của tam giác ABI ==> I1 = BAI + B1 = C2 + A1

Vậy  BAC = BPD = 2 (C2 + A1)

Góc ngoài DPC của tam giác APC ==> DPC =  C2 + A1

nên BAC = 2 DPC

Phần a) chứng minh BP = 2AP ở trên, có thể dùng định lý hàm số sin trong tam giác để giải như sau:

Định lý hàm số sin trong BAD cho ta: BD/sin(A2) = AB/sin(D1) (1)

Ðịnh lý hàm số sin trong  CAD cho ta: DC/sin(A1) = AC/sin(D2) (2)

Chia (1) cho (2) ta được:

BD.sin(A1)/sin(A2).DC =  AB.sin(D2)/sin(D1).AC

Theo tính chất của cung liên kết: sin(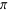-x) = sin x, thì sin(D2) = sin(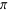-D1) = sin(D1); và theo giả thiết AB=AC nên vế 2 của đẳng thức trên bằng 1, vậy vế 1 là: 

BD.sin(A1)/sin(A2).DC = 1. Vì BD = 2DC, suy ra: sin(A1)/(sin(A2)= ½ (3)

Trong ABP, ta có BPD = B1 + A2 (góc ngoài bằng hai góc trong không kề với nó). A = A1 + A2

Theo giả thiết: BPD = A, vậy B1 = A1

Cũng trong ABP, định lý hàm số sin cho ta: BP/sin(A2) = AP/sin(B1)

Vì B1 = A1 nên đẳng thức trên cũng có thể viết:

sin(A1)/sin(A2) = AP/BP (4)

So sánh (3) và (4) ta được AP/BP = ½ ==> BP = 2 AP

:: Bài 12

Cho hình lục giác ABCDEF nội tiếp trong vòng tròn tâm O bán kính R với AB = CD = EF = R. M, N, P tuần tự là trung điểm của BC, DE, FA. Chứng Minh: MNP là tam giác đều.

BÀI GIẢI

Gọi G, H, I, J lần lượt à trung điểm các bán kính OA, OB, OC, OD. Hai tam giác cân GHM và JIM có:  HG = HM = IJ = IM = R/2, và: I = I1 + I2 = 120^o + = H1 + H2 = H

Vậy chúng bằng nhau. Suy ra: GM = JM (1)    

Tổng các góc trong JIM là:

I1 + I2 + 2 = 180^o

120^o + +2 = 180^o

==> 2 = 180^o - 120^o - = 60^o -

==> = 30^o - /2

Ta có: PGM = G1 + G2 + G3

= (180^o - ) + 60^o +

= 240^o - + (30^o - /2)

= 270^o - - /2

NJM = J1 +J2

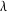= + (120^o - )

= (180^o - - ) +120^o - (30^o - /2)

= 270^o - - /2

Vậy PGM = NJM (2)

Hai tam giác PGM và NJM có hai cạnh bằng nhau (PG = NJ (= R/2), GM = JM (1)) kèm giữa một góc bằng nhau (PGM = NJM (2)), vậy chúng bằng nhau. Suy ra: PM = NM.

Nối thêm với các trung điểm của OE, OF và chứng minh tương tự như trên, ta sẽ được: PM = NM = PN.

Vậy: tam giác MNP đều.

:: Bài 13

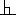I và O theo thứ tự là tâm vòng nội tiếp và ngoại tiếp của tam giác ABC. Chứng minh rằng nếu EA = AB = BD và C = 30^o thì ED = IO và ED IO. (Trích từ "Gux Mathematicorum", 1987).

BÀI GIẢI

Nối dài đường phân giác AI cắt vòng tròn ngoại tiếp ABC tại F. F chính là trung điểm cung BC, vậy FO 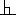BC.   

Vì EAB cân nên AF cũng là đường trung trực của EB, suy ra FE = FB; 

AFB = C = 30^o  ==> EFB đều, ==> FB = BE (1).

Ðể ý AIB, góc ngoài FIB bằng tổng số hai góc trong không kề với nó, vậy:

FIB = IAB + IBA = A/2 + B/2 

Ta cũng có: FBI = FBC + CBI = FAC + CBI = A/2 + B/2

Vậy BFI cân ==> FB = FI (2)

Từ (1) và (2) ta có: BE = FI.

Theo giả thiết C = 30^o ==> 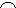AB = 60^o ==> AB = R ==> DB = OF

Hai tam giác DBE và OFI bằng nhau vì: BE = FI, DB = OF và OFI = CBE (góc có cạnh thẳng góc: BE 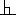FI, FO 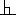BC).   

Suy ra:  ED = IO và BED = FIO.

Theo trên BED = FIO, mà BE 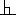FI, vậy ED 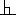IO. 

:: Bài 14

Tam giác ABC có vòng tròn nội tiếp tâm O. D là tiếp điểm và M là trung điểm của BC. Chứng minh rằng MO cắt AD tại trung điểm I.

BÀI GIẢI

Vẽ đường kính DD'. Qua D' vẽ B'C' // BC,

==> AB'C' ~ ABC

==> vòng tròn nội tiếp AB'C' tiếp xúc với B'C' tại điểm K trên AD.

Các tiếp tuyến phát xuất từ một điểm đến vòng tròn thì bằng nhau nên ta có: EF = GH. ==> EF = B'E + B'F = B'K + B'D' = B'K + (B'K + KD')

==> EF = 2B'K + KD' (1)

GH = C'G + C'H = C'K + C'D' = (C'D'+D'K) + C'D'

==> GH = 2C'D' + KD' (2)

Theo trên ta có EF = GH nên (1) = (2) suy ra B'K = C'D' cũng có nghĩa BD = CN vì AB'C' ~ ABC, vậy M là trung điểm của DN (vì M đã là trung điểm của BC theo giả thiết).

M, O lần lượt là trung điểm của DN và DD' nên MO // ND' ==> MI // NA.

Trong ADN, MI // NA và M là trung điểm của DN thì I phải là trung điểm của DA và MI = 1/2 NA. Kết luận: MO cắt AD tại trung điểm I

:: Bài 15

Nếu : AB + BF = AD + DF thì: AC + CF = AE + EF

BÀI GIẢI

Trên AB kéo dài lấy điểm P sao cho BP = BF. Trên AD kéo dài lấy điểm M sao cho DM = DF. Vậy giả thiết cho AB+BF=AD+DF cũng tương tự giả thiết cho AP = AM ==> PAM cân.

Trên AC kéo dài lấy điểm Q sao cho CQ = CF. Trên AE kéo dài lấy điểm N sao cho EN = EF. Vậy chứng minh AC+CF=AE+EF cũng tương tự chứng minh AQ = AN.

Vẽ 3 đường phân giác của 3 góc A, B, D và gọi , , là nửa số đo các góc ấy. Ba đường phân giác trên cũng chính là 3 đường cao của 3 tam giác cân PAM, PBF, MDF.

Ta có:

FMP = AMP - AMF = (90^o- ) - (90^o- ) = - (1)

FPM = APM - APF = (90^o - ) - (90^o- ) = - (2)

QCF = ADC + A = (180^o- 2) + 2

Q = (180^o - QCF)/2 = (180^o- (180^o- 2+2))/2 = -  (3)

Từ (1) & (3) ==> FMP = Q, chứng tỏ 4 điểm Q, P, F, M ở trên một vòng tròn.  

NEF = ABE + A = (180^o- 2) + 2

N = (180^o -NEF)/2 = (180^o- (180^o- 2+ 2))/2 = - (4)           

Từ (2) & (4) ==> FPM = N, chứng tỏ 4 điểm P, F, M, N ở trên một vòng tròn. Vậy vòng tròn đi qua 5 điểm Q, P, F, M, N.

PFQ = 180^o- (FPQ + Q) = 180^o- (90^o ++- ) = 90^o--+  

MFN =180^o- (FMN +N) =180^o-(90^o ++- ) = 90^o--+

Vậy PFQ = MFN, nên chúng cũng chắn hai dây cung bằng nhau PQ và MN.    

Ta đã có AP = AM theo giả thiết, vậy AQ = AN.

Kết Luận: AC + CF = AE + EF

:: Bài 16

Cho tam giác ABC với AB > BC, BM là trung tuyến và BL là phân giác. Ðường thẳng qua M song song với AB cắt BL tại D. Ðường thẳng qua L song song với BC cắt BM tại E. Chứng minh: ED thẳng góc với BL. (Vô địch Liên Xô năm 1998)

BÀI GIẢI

Kéo dài MD cắt BC tại F. Vì MD // AB và M là trung điểm của AC (giả thiết) nên F cũng là trung điểm của BC. Theo giả thiết: EL // BC nên MD cũng cắt EL tại trung điểm. Vậy GE = GL (1)

Ta có:

LBF = BLE (so le trong)

LBA = LDM (đồng vị)

suy ra: BLE = LDM ==> GDL cân ==> DG = GL (2).

Từ (1) và (2) ta có: DG = GL = GE.

Xét tam giác EDL, đường trung tuyến DG = 1/2 EL; chứng tỏ EDL là một tam giác vuông.

Vậy: ED BL 

:: Bài 17

Cho tam giác ABC với A = 2 B. Trung trực của AB kẻ từ M cắt BC, AC tại E và F. Ðường thẳng góc với BC tại B cắt AC tại D. Chứng minh: AMC = DMB

BÀI GIẢI

Giả thiết cho A = 2 ABC và E, F nằm trên đường trung trực của AB, suy ra AE là phân giác của góc A và BE cũng là phân giác của góc ABF.

Ðường thẳng DM cắt 3 cạnh của tam giác AFB tại D, G, M; theo định lý Menelaus:

(http://mathworld.wolfram.com/MenelausTheorem.html  &  http://www.mathpages.com/rr/s3-09/3-09.htm)

ta có hệ thức: AD. FG. BM = FD. BG. AM

Suy ra: AD / FD = BG / FG (1) 

Theo giả thiết: BD BC nên BD là phân giác ngoài của AFB nên ta có: AD / FD = BA / BF = BA / FA (2)                 

Từ (1) và (2) suy ra: BG / FG = BA / FA    

Hệ thức này chứng tỏ AG là phân giác của góc A. Vậy đường AE nối dài phải qua G và G chính là điểm đối xứng với C qua trung trực MF. 

Kết luận:  AMC = DMB

:: Bài 18

Cho hai vòng tròn tâm A, B cắt nhau ở M và N. Hai đường tiếp tuyến chung của chúng cắt AB tại D. Hai bán kính AP // BQ. PQ cắt AB tại C. Chứng minh: CND = 90^o.

(Trích từ Challenging Problems in Geometry, Alfred S. Posamentier & Charles T. Salkind, Dover Publications Inc., NY, 1988, trang 141)

BÀI GIẢI

AB, PQ tạo với hai đường song song AP, BQ những góc so le trong bằng nhau nên hai tam giác APC và BQC đồng dạng; ta có hệ thức:

CA / CB = AP / BQ ==>

CA / CB = AN / BN

Hệ thức này chứng tỏ trong tam giác ANB, NC là đường phân giác của góc ANB.

Vì AE // BF nên hai tam giác ADE và BDF đồng dạng, ta có hệ thức:

DA / DB = AE / BF ==>

DA / DB = AN / BN

Hệ thức này chứng tỏ trong tam giác ANB, ND là đường phân giác của góc ngoài ở N (BNk)

Hai đường phân giác trong và ngoài nêu trên thẳng góc với nhau.

Vậy: CND = 90^o

:: Bài 19

Ba giao điểm của các đường thẳng chia đều mỗi góc của một tam giác làm 3 phần hợp thành một tam giác đều. (Ðịnh lý Morley (*) này cũng đúng cho góc ngoài:  http://mathworld.wolfram.com/MorleysTheorem.html)  

Giả thiết: A1 = A2 =A3, B1 = B2 = B3, C1 = C2 = C3

Kết Luận: DEF đều.

BÀI GIẢI

Ta có thể chứng minh ngược lại rằng nếu DEF đều thì: 

A1 = A2 =A3

B1 = B2 = B3

C1 = C2 = C3

Vẽ tam giác đều DEF. Trên các cạnh của nó, dựng những tam giác cân D'FE, F'ED, E'DF có góc đáy theo thứ tự là , , ; sao cho + + = 120^o và < 60^o , < 60^o , < 60^o . Kéo dài những cạnh của các tam giác cân nêu trên, chúng gặp nhau tại A, B, C.

Do + + + 60^o = 180^o , ta có thể suy ra số đo những góc khác; chẳng hạn trong AEF, góc ở đỉnh A (A2) phải là 60^o - , thì góc ở đỉnh E và F lần lượt sẽ là + và +.

Vì D', D cách đều E và F nên D'D là trung trực của EF và cũng là phân giác của ED'F. Vậy D'D là một phân giác của BD'C. Tâm vòng tròn nội tiếp của BD'C phải nằm trên đường phân giác này (tâm vòng nội tiếp là giao điểm của 3 đường phân giác). 

Mặt khác, rút từ tính chất của tâm vòng nội tiếp, nếu ta chứng minh được:

BDC = 90^o  + ½ BD'C thì D chính là tâm vòng tròn nội tiếp của BD'C.

Thật vậy: 1/2 BD'C = ½ ED'F = 90^o -

BDC = 180^o - = 90^o + (90^o - ) = 90^o + ½ BD'C

Vậy D là tâm vòng nội tiếp của BD'C ==> B2 = B3 và C1 = C2.

Cũng chứng minh tương tự, ta được:

E là tâm vòng nội tiếp của AE'B ==> A1 = A2 và B1 = B2

F là tâm vòng nội tiếp của AF'C ==> A2 = A3 và C2 = C3.

Kết luận: Mỗi góc của ABC đã được chia đều làm 3 góc nhỏ.

(*) Morley's Theorem: The three points of intersection of the adjacent trisectors of the angles of any triangle form an equilateral triangle.

:: Bài 20

Cho tam giác đều ABC. Kẻ đường thẳng bất kỳ song song với AC, cắt AB và BC tại E và F. Gọi G là tâm của BEF, M là trung điểm của AF. Tính các góc của GMC.

BÀI GIẢI

Giả thiết cho EF // AC nên BEF cũng đều. Kéo dài BG gặp AC tại K ==>GKC vuông và K là trung điểm của AC.  

K, M, N lần lượt là trung điểm của AC, AF, EF và FC = EA ==> MK = NM ==> K1 = N1 = 30^o. 

Suy ra: MKC = 120^o.

Ta cũng có MDC = B = 60^o (góc đồng vị). Tứ giác DMKC có hai góc đối MKC và MDC bù nhau, vậy nội tiếp được trong một vòng tròn. Vòng tròn này cũng qua G vì GDC và GKC đều vuông.

Tóm lại năm điểm D, G, M, K, C cùng nằm trên vòng tròn đường kính GC.

Vậy GMC = 90^o.

MGC = MDC = 60^o và MCG = 30^o.

Kết Luận: GMC = 90^o, MGC = 60^o, MCG = 30^o.

T. V. Phê & Nguyễn Tin