|
|
|
|
|
VĂN HỌC |
GIAI THOẠI | TIỂU LUÂN | THƠ | TRUYỆN | THỜI LUẬN | NHÂN VẬT | ÂM NHẠC | HỘI HỌA | KHOA HỌC | GIẢI TRÍ | TIỂU SỬ |
-
Link Tác Phẩm và Tác Giả Tác Phẩm
Tác Giả
Thơ Văn Trần Y. Hoa & Bằng hữu
Thơ Văn Trần Yên Hoà & Bằng hữu
Tạp Chí
PHONG HÓA & NGÀY NAY
(Đại học Hoa Sen)
TỰ LỰC VĂN ĐOÀN, tác phẩm
(Viện Việt Học)
VĂN HỌC
Tạp chí Văn Học
DÒNG VIỆT
Trọn bộ DÒNG VIỆT
(1993-2009)
VĂN (Xuân Canh Thìn)
(vanmagazine)
TIỂU THUYẾT THỨ BẢY
NAM PHONG - TRI TÂN
THANH NGHỊ - NGÀY NAY
VĂN HOÁ NGÀY NAY
TẬP SAN SỬ ĐỊA
THẾ KỶ 21 - BÁCH KHOA
Tạp Chí VHNT Miền Nam
TÂN VĂN
TIN VĂN
Tạp chí ĐỌC VÀ VIẾT
THƯ QUÁN BẢN THẢO
Sách Xưa
• QUỐC VĂN GIÁO KHOA THƯ:
- Lớp Sơ Đẳng
- Lớp Đồng Ấu
- Lớp Dự Bị
• TỦ SÁCH TIẾNG VIỆT
• KHO SÁCH XƯA
• QUÁN VEN ĐƯỜNG
• LITTLE SAIGON
Phim và Hình Ảnh Xưa
- Cuộc Di Cư Năm 1954
- Phim "Chúng Tôi Muốn Sống"
- Phim "Nắng Chiều", 1973
- Phim Chân Trời Tím, 1971
- Hình ảnh xưa
eBooks
-
Giải Đề Thi Toán Quốc Tế môn Hinh Hoc -2 (Học Xá) Ad-23-Index Ad-23-Index = (Ad-23-468x60created-2-1-10) (Học Xá)
24-7-2011 | KHOA HỌC
Giải Đề Thi Toán Quốc Tế (Hình Học) các năm 2000 ... 2004
HỌC XÁ
Share File.php Share File




2000 (IMO 41th) 2001 (IMO 42th) 2002 (IMO 43th) 2003 (IMO 44th) 2004 (IMO 45th)
:: IMO 41th (2000, Korea)
(http://www.imo-official.org/year_info.aspx?year=2000)
Cho hai vòng tròn cắt nhau tại M và N với AB là tiếp tuyến chung gần điểm M. Qua M vẽ một cát tuyến song song với AB cắt hai vòng trên tại C và D. AN và BN cắt CD tại P và Q; CA và DB giao nhau tại E. Chứng Minh: PE = QE.
(AB is tangent to the circles CAMN and NMBD. M lies between C and D on the line CD, and CD is parallel to AB. The chords NA and CM meet at P; the chords NB and MD meet at Q. The rays CA and DB meet at E. Prove that PE = QE).
BÀI GIẢI
 AB // CD (theo giả thiết) nên
AB // CD (theo giả thiết) nên  EBA =
EBA =  EDC (góc đồng vị) (1)
EDC (góc đồng vị) (1)
AB là tiếp tuyến với vòng
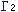 nên
nên  ABM =
ABM =  BDM (cùng chắn cung BM) (2).
BDM (cùng chắn cung BM) (2).
Từ (1) và (2) cho:
 EBA =
EBA =  ABM
ABM
Cũng chứng minh tương tự, ta có:
 EAB =
EAB =  BAM. Do vậy
BAM. Do vậy  EAB =
EAB =  MAB ==> AE = AM ==>
MAB ==> AE = AM ==>  EAJ =
EAJ =  MAJ ==>
MAJ ==>  AJE =
AJE =  AJM, suy ra EM
AJM, suy ra EM  AB ==> EM
AB ==> EM  PQ (3)
PQ (3)
IA là tiếp tuyến của vòng
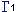 và IB là tiếp tuyến của vòng
và IB là tiếp tuyến của vòng 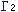 nên ta có: IA2 = IM . IN = IB2 ==> IA = IB ==> MP = MQ (vì PQ // AB) (4)
nên ta có: IA2 = IM . IN = IB2 ==> IA = IB ==> MP = MQ (vì PQ // AB) (4)
Tam giác EPQ có EM là đường cao (3) và cũng là đường trung tuyến (4), vậy là tam giác cân; suy ra: PE = QE
Ad-23-Index Ad-23-Index = (Ad-23-468x60created-2-1-10) (Học Xá)
:: IMO 42th (2001, United States of America)
(http://www.imo-official.org/year_info.aspx?year=2001)
Tam giác ABC có 3 góc nhọn. O là tâm vòng tròn ngoại tiếp. P là chân đường cao kẻ từ A xuống BC. Cho
 BCA
BCA 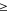
 ABC + 30o. Chứng minh:
ABC + 30o. Chứng minh:  CAB +
CAB +  COP < 90o.
COP < 90o.
(Let ABC be an acute-angled triangle with circumcenter O. Let P on BC be the foot of the altitude from A. Suppose that
 BCA
BCA 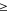
 ABC + 30o. Prove that
ABC + 30o. Prove that  CAB +
CAB +  COP < 90o).
COP < 90o).
BÀI GIẢI
 Từ A vẽ đoạn thẳng song song với BC cắt vòng tròn tại D, vậy ADBC là hình thang cân có hai góc đáy bằng nhau:
Từ A vẽ đoạn thẳng song song với BC cắt vòng tròn tại D, vậy ADBC là hình thang cân có hai góc đáy bằng nhau:  C =
C =  ABC +
ABC +  ABD
ABD
Vì
 C
C 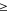
 ABC + 30o (theo giả thiiết)
ABC + 30o (theo giả thiiết)nên
 ABC +
ABC +  ABD
ABD 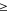
 ABC + 30o ==> ABD
ABC + 30o ==> ABD 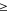 30o ==>
30o ==>  AOD
AOD 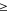 60o ==> DA
60o ==> DA 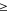 R (bán kính vòng O).
R (bán kính vòng O).
Gọi I, J là trung điểm của AD và BC, ta có: IA = JP
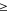 R/2.
R/2.
Trong một tam giác vuông, đường huyền dài hơn mỗi cạnh nên OP > JP
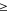 R/2 (1). Cũng vậy, trong tam giác vuông OJC ta có JC < OC ==> JC < R.
R/2 (1). Cũng vậy, trong tam giác vuông OJC ta có JC < OC ==> JC < R.
Ðể ý hiệu số JC - JP . Theo kết quả tính ở trên: giới hạn của JC là R, vậy nếu JP
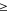 R/2 thì JC - JP < R/2 ==> PC < R/2 (2).
R/2 thì JC - JP < R/2 ==> PC < R/2 (2).
Kéo dài bán kính CO gặp vòng tròn tại E. Trong một tam giác, cạnh lớn đối diện với góc lớn và ngược lại, nên từ (1) và (2) suy ra OP > PC ==>
 PCO >
PCO >  COP ==>
COP ==>  BAE >
BAE > COP.
COP.
Vậy nếu
 CAB +
CAB +  BAE = 90o (góc nội tiếp trong nửa vòng O),
BAE = 90o (góc nội tiếp trong nửa vòng O),
thì:
 CAB +
CAB +  COP < 90o.
COP < 90o.
Ad-22-A_Newest-Feb25-2022 Ad-22-A_Newest-Feb25-2022
:: IMO 43th (2002, United Kingdom)
(http://www.imo-official.org/year_info.aspx?year=2002)
Cho nửa vòng tròn tâm O đường kính BC. Chọn điểm A trên nửavòng (O) sao cho
 AOC > 60o. EF là trung trực của AO. D là trung điểm cung AB. Kẻ đường thẳng qua O song song với AD gặp AC tại J. Chứng minh J là tâm vòng nội tiếp của tam giác CEF.
AOC > 60o. EF là trung trực của AO. D là trung điểm cung AB. Kẻ đường thẳng qua O song song với AD gặp AC tại J. Chứng minh J là tâm vòng nội tiếp của tam giác CEF.
(BC is a diameter of a circle center O. A is any point on the circle with
 AOC > 60o. EF is the chord which is the perpendicular bisector of AO. D is the midpoint of the minor arc AB. The line through O parallel to AD meets AC at J. Show that J is the incenter of triangle CEF).
AOC > 60o. EF is the chord which is the perpendicular bisector of AO. D is the midpoint of the minor arc AB. The line through O parallel to AD meets AC at J. Show that J is the incenter of triangle CEF).
BÀI GIẢI

 BOD =
1/2
BOD =
1/2 BOA (theo giả thiết)
BOA (theo giả thiết)
 BCA = 1/2
BCA = 1/2 BOA (góc ở tâm vòng tròn)
BOA (góc ở tâm vòng tròn)
Vậy
 BOD =
BOD =  BCA ==> OD // CA.
BCA ==> OD // CA.
Ta còn có: OJ // AD (theo giả thiết).
Vậy tứ giác OJAD là hình bình hành, suy ra: AJ = OD = R.
Theo giả thiết: EF là trung trực của OA, vậy: AF = OF = R và AE = OE = R.
Tóm lại: AF=AJ=AE=AO=R, chứng tỏ tứ giác FJOE nội tiếp trong vòng tròn tâm A bán kính AO = R.
Theo trên ta có AF = AE = R ==>
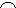 AF =
AF = 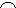 AE, suy ra
AE, suy ra  FCA =
FCA =  ACE, vậy CA là đường phân giác của góc C trong tam giác CEF.
ACE, vậy CA là đường phân giác của góc C trong tam giác CEF.
Với vòng tròn tâm A, ta có
 EFJ = 1/2
EFJ = 1/2 EAJ (góc ở tâm vòng (A))
EAJ (góc ở tâm vòng (A))
Với vòng tròn tâm O, ta có
 EAJ =
EAJ =  EFC ==>
EFC ==>  EFJ = 1/2
EFJ = 1/2 EFC, vậy FJ cũng là đường phân giác của góc F trong tam giác CEF.
EFC, vậy FJ cũng là đường phân giác của góc F trong tam giác CEF.
Kết luận: J là giao điểm các đường phân giác trong của tam giác CEF, đó chính là tâm vòng tròn nội tiếp của tam giác CEF.
Ad-23-Index Ad-23-Index = (Ad-23-468x60created-2-1-10) (Học Xá)
:: IMO 44th (2003, Japan)
(http://www.imo-official.org/year_info.aspx?year=2003)
Cho tứ giác nội tiếp ABCD. P, Q, R theo thứ tự là chân các đường cao từ D xuống AB, BC, CA. Chứng minh rằng RP = RQ nếu và chỉ nếu phân giác của hai góc ABC và ADC cắt nhau trên AC.
(ABCD is cyclic. The feet of the perpendicular from D to the lines AB, BC, CA are P, Q, R respectively. Show that the angle bisectors of ABC and CDA meet on the line AC iff RP = RQ).
BÀI GIẢI
 Ta có:
Ta có:  R1 =
R1 =  D1 (cùng chắn cung CQ của vòng ngoại tiếp tứ giác CQDR),
D1 (cùng chắn cung CQ của vòng ngoại tiếp tứ giác CQDR),  R2 =
R2 =  D2 (cùng chắn cung AP của vòng ngoại tiếp tứ giác APRD).
D2 (cùng chắn cung AP của vòng ngoại tiếp tứ giác APRD).
Vì:
 D1 =
D1 =  D2 (cùng phụ cho 2 góc bằng nhau DCQ và A),
nên
D2 (cùng phụ cho 2 góc bằng nhau DCQ và A),
nên  R1 =
R1 =  R2; chứng tỏ P, R, Q thẳng hàng. Ðó chính là đường thẳng Simson (*).
R2; chứng tỏ P, R, Q thẳng hàng. Ðó chính là đường thẳng Simson (*).
 DAB ~
DAB ~  DRQ vì
DRQ vì  DAB =
DAB = DCQ =
DCQ = DRQ và
DRQ và  DBA =
DBA =  DCA =
DCA =  DQR
DQR ==> DA / AB = DR / RQ
 DBC ~
DBC ~  DPR vì
DPR vì  DBC =
DBC = DAC =
DAC = DPR và
DPR và  CDB =
CDB =  CAB =
CAB =  RDP
RDP ==> DC / BC = DR / PR
Vậy: DA/DC = [AB(DR/RQ)]/[BC(DR/PR)]= (AB/BC).PR/RQ (1)
Nếu RP = RQ thì PR / RQ = 1 và (1) sẽ là: DA / DC = BA / BC. Tỷ số này chứng tỏ hai đường phân giác cuả hai góc ABC và ADC cắt nhau trên AC và ngược lại.
(*) (http://mathworld.wolfram.com/SimsonLine.html)
Ad-22-A_Newest-Feb25-2022 Ad-22-A_Newest-Feb25-2022
:: IMO 45th (2004, Greece)
(http://www.imo-official.org/year_info.aspx?year=2004)
1. Cho tam giác ABC với các góc nhọn và AB
 AC. Vòng tròn đường kính BC tâm O cắt AB, AC lần lượt tại M và N. Phân giác trong của góc BAC và MON gặp nhau tại R. Chứng minh rằng vòng tròn ngoại tiếp của hai tam giác BMR và CNR có một điểm chung nằm trên BC.
AC. Vòng tròn đường kính BC tâm O cắt AB, AC lần lượt tại M và N. Phân giác trong của góc BAC và MON gặp nhau tại R. Chứng minh rằng vòng tròn ngoại tiếp của hai tam giác BMR và CNR có một điểm chung nằm trên BC.(Let ABC be an acute-angled triangle with AB
 AC. The circle with diameter BC intersects the sides AB and AC at M and N respectively. Denote by O the midpoint of the side BC. The bisectors of the angles BAC and MON intersect at R. Prove that the circumcircles of the triangles BMR and CNR have a common point lying on the side BC) http://www.imo-register.org.uk/2004-report.html
AC. The circle with diameter BC intersects the sides AB and AC at M and N respectively. Denote by O the midpoint of the side BC. The bisectors of the angles BAC and MON intersect at R. Prove that the circumcircles of the triangles BMR and CNR have a common point lying on the side BC) http://www.imo-register.org.uk/2004-report.html
BÀI GIẢI
 Với vòng tròn tâm O, ta có:
Với vòng tròn tâm O, ta có:  MNA =
MNA =  B (cùng chắn cung MC).
B (cùng chắn cung MC).
Tam giác CON cân ==>
 ONC =
ONC =  C, vậy
C, vậy  ONM =
ONM =  A =
A =  , chứng tỏ ON là tiếp tuyến của vòng tròn tâm I ngoại tiếp với
, chứng tỏ ON là tiếp tuyến của vòng tròn tâm I ngoại tiếp với  AMN.
AMN.
Tương tự như thế với OM nên tam giác MON cân. Theo giả thiết OR là phân giác cũng là trung trực của
 MON ==>
MON ==>  MRN cân, vậy MR, NR cũng là hai đường phân giác khác của
MRN cân, vậy MR, NR cũng là hai đường phân giác khác của  MON; Chứng tỏ R là tâm vòng tròn nội tiếp với
MON; Chứng tỏ R là tâm vòng tròn nội tiếp với  MON. R cũng là trung điểm cung MN thuộc vòng tròn tâm I.
MON. R cũng là trung điểm cung MN thuộc vòng tròn tâm I.
Hai vòng tròn tâm J và K ngoại tiếp với hai tam giác BMR và CNR có điểm chung thứ hai là P.
Ta có: AMB là trục đẳng phương của hai vòng tròn tâm J và O,
ANC là trục đẳng phương của hai vòng tròn tâm K và O,
nên ARP là trục đẳng phương của hai vòng tròn tâm J và K.
Vậy A,R,P thẳng hàng. Tứ giác nội tiếp PRMB và PRNC cho:
 RPB +
RPB +  RMB =
RMB =  RPB +
RPB +  B +
B +  A/2 = 180o
A/2 = 180o
 RPC +
RPC +  RNC =
RNC =  RPC +
RPC +  C +
C +  A/2 = 180o
A/2 = 180o
==>
 RPB +
RPB +  RPC = 180o. Vậy P phải nằm trên BC.
RPC = 180o. Vậy P phải nằm trên BC.
Ad-23-Index Ad-23-Index = (Ad-23-468x60created-2-1-10) (Học Xá)
2. Cho tứ giác lồi ABCD với đường chép BD không phải là phân giác của góc ABC và góc CDA. Một điểm P nằm trong tứ giác sao cho:
 PBC =
PBC =  DBA,
DBA,  PDC =
PDC =  BDA. Chứng minh rằng ABCD là một tứ giác nội tiếp nếu và chỉ nếu AP = CP.
BDA. Chứng minh rằng ABCD là một tứ giác nội tiếp nếu và chỉ nếu AP = CP.
(In a convex quadrilateral ABCD the diagonal BD does not bisect the angles ABC and CDA. The point P lies inside ABCD and satisfies
 PBC =
PBC =  DBA and
DBA and  PDC =
PDC =  BDA. Prove that ABCD is a cyclic quadrilateral if and only if AP = CP).
BDA. Prove that ABCD is a cyclic quadrilateral if and only if AP = CP).
BÀI GIẢI
 Chọn điểm P nằm trong hai tam giác ABD và ACD.
Chọn điểm P nằm trong hai tam giác ABD và ACD.
1) Phần thuận: Nếu tứ giác ABCD nội tiếp thì AP = CP:
Kẻ đường thẳng BP và DP cắt AC lần lượt tại G và H. Theo giả thiết và dựa vào những góc cùng chắn cung, ta có ba tam giác BAD, BGC, CHD có hai góc bằng nhau từng đôi một nên chúng đồng dạng.
Suy ra tỷ số: GC / BC = AD / BD (1)
và
 BGC =
BGC =  CHD ==>
CHD ==>  PGH cân
PGH cân
==> PG = PH và
 AHP =
AHP =  CGP.
CGP.
Cũng vậy, hai tam giác ADH và BDC đồng dạng, cho ta tỷ số: AH / BC = AD / BD (2).
Từ (1) và (2) ==> GC = AH
Do đó
 AHP =
AHP =  CGP. Vậy: AP = CP.
CGP. Vậy: AP = CP.
 2) Phần đảo: Nếu AP = CP thì tứ giác ABCD nội tiếp:
2) Phần đảo: Nếu AP = CP thì tứ giác ABCD nội tiếp:
Vẽ vòng tròn nội tiếp
 BCP cắt CD và DP lần lượt tại E và F. Theo giả thiết và dựa vào những góc cùng chắn cung, ta có:
BCP cắt CD và DP lần lượt tại E và F. Theo giả thiết và dựa vào những góc cùng chắn cung, ta có:  ADB ~
ADB ~  PDE
PDE
==> AD / BD = PD / ED (3),
suy ra:
 ADP ~
ADP ~  BDE (
BDE ( ADP =
ADP =  BDE kèm giữa hai cặp cạnh tỷ lệ(3)),
BDE kèm giữa hai cặp cạnh tỷ lệ(3)),
==> AP / BE = DP / DE (4)
Ta cũng có:
 DCP ~
DCP ~  DFE
DFE ==> CP / FE = DP / DE (5)
Từ (4) và (5) và theo giả thiết AP = CP nên: BE = FE ==>
 FBE =
FBE =  BFE.
BFE.
Tứ giác nội tiếp BFEC cho ta:
 BFE +
BFE +  BCE
= 180o Thế mà
BCE
= 180o Thế mà  BFE =
BFE =  FBE =
FBE =  EPD =
EPD =  BAD
BAD
Vậy
 BAD +
BAD +  BCD = 180o. Ðiều này chứng tỏ: Tứ giác ABCD nội tiếp.
BCD = 180o. Ðiều này chứng tỏ: Tứ giác ABCD nội tiếp.
Kết Luận: Tứ giác ABCD nội tiếp nếu và chỉ nếu AP = CP.
Ad-22-A_Newest-Feb25-2022 Ad-22-A_Newest-Feb25-2022
-
Bài Khảo Cứu & Bài Tập Hình Học (Học Xá) • Bài Khảo Cứu
Cùng Mục (Link) • Có Và Không Của Thế Gian (Hoàng Dung)
• DNA, Đặc Tính Sự Sống và Sinh Vật (Hoàng Dung)
• Thử Tìm Hiểu ChatGPT (Đào Như)
• Những khám phá mới về Chất Trắng Trong Não Bộ (Trần Hồng Văn)
• Siêu Thượng Không Gian: Chương Kết Luận (Trà Nguyễn)
• Vài Mạn Đàm Về Sao Trời (Hoàng Dung)
• Vật Lý Lượng Tử Và Ý Nghĩa Thiền Học Của Vật Chất (Hoàng Dung)
• Những Quan Niệm và Học Thuyết Mới về Vũ Trụ (Phần 2) (Trần Hồng Văn)
• Những Quan Niệm và Học Thuyết Mới về Vũ Trụ (Phần 1) (Trần Hồng Văn)
• “Mỹ Ngữ” Và “Anh Ngữ” Khác Nhau Thế Nào? (Đàm Trung Pháp)

• Hình Học (Bài Tập)
Bài 48 (Điểm Schiffler của tam giác)
Bài IOM: 7 - 38, 41 - 45, 46 - 51
• Anh Ngữ
• Đố Vui: 1, 2
Liên Kết Trong Mục Học Toán (Học Xá) Liên Kết
IMO
Wolfram MathWorld
The Math Forum
USAmts
Komal
MathLinks
Cut-The-Knot
Từ Điển Anh Việt
|
© Hoc Xá 2002 (T.V. Phê - phevtran@gmail.com) |
















