12-9-2011 | KHOA HỌC

Đố Vui - 1

  NHIỀU TÁC GIẢ

Puzzle (1):

YIN OR YANG (by CLIFFORD A. PICKOVER)

CONFUCUS, the great Chinese philosopher, is preparing a birthday cake for a friend's twin sons. He knows that one prefers chocolates, while the other prefers vanilla. Confucius, in his wisdom, bakes a cake in the shape of the ancient yin-yang symbol of two opposing cosmic forces. He knows this should satisfy the children because the symbol is, geometrically speaking, a circle divided into two equal parts, and one part of the cake is chocolate, the other vanilla. Confucius cuts the cake into two pieces along the curvy line dividing the two flavors. When the children come and look at the cake, they cry, "Oh Great One, there are four children to serve, not just two. Two of us like chocolate, and two of us like vanilla." Confucius sighs. "Okay, there is a way to cut the cake into four pieces of the same size and shape using just one more vertical cut. If you can figure out how to make such a cut, the four of you will be satisfied." Can you help the children divide the yin and the yang into four pieces of identical shape and size with a single vertical cut? (DISCOVER Magazine)

Solution :

This puzzle is actually based on an ancient problem, and shown here is the only solution of which I am aware. To satisfy yourself that the pieces are in fact the same size and shape, you can draw this pattern on a piece of paper, cut out the pieces, and superimpose them on one another. It's also possible for the children to divide the yin and the yang into four pieces with the same area but different shapes by a single extra cut. Can you figure out how? Please send your answers to Clifford A. Pickover, c/o DISCOVER, 114 Fifth Avenue, New York, N.Y. 10011-5690.

Puzzle (2):

SIRIUS GEOMETRY (by CLIFFORD A. PICKOVER)

Aliens from a planet circling the star Sirius have abducted a Kansas City mill worker in order to acess his intelligence. Their ship is now located at position S in the diagram below. The aliens wish to travel to a plasmoid wall in space called the Continuum for the purpose of refueling their ship using energy from the wall. After this they wish to travel to a star called Aleph-naught, devoted by A. They tell the abductee, "We wish to travel to the edge of the Continuum for refueling, then to Aleph-naught, traveling as short a distance as possible. To what point on the edge of the Continuum should we travel?" (DISCOVER Magazine)

Solution :

Suppose that the aliens aim for some point P on the edge of the Continuum. Create a reflection of S in the Continuum and call it S'. Then the distance SPA equals S'PA, which will be shortest when S'PA is a straight line. It follows that P is the point such that SP and PA make the same angle with the edge of the Continuum.

(In the first century A. D., Hero of Alexandria used a similar argument to conclude that when light is reflected from a mirror, the angles of incidence and reflection are equal).

Puzzle (3):

FAMILLY VALUES (by RAYMOND SMULLYAN)

1. Eldon White has four dogs. One day he put out a bowl of dog biscuits. The eldest dog came first and ate half the biscuits plus one more. Then the next dog came and ate half of what he found plus one more. Then the next one came and ate half of what she found plus one more. Then the little one came and ate half of what she found and one more, and that finished the biscuits. How many biscuits were originally in the bowl?

2. Eldon once bought a very remarkable plant, which, on the first day, increased its height by a half, on the second day by a third, on the third day by a quarter, and so on. How many days did it take to grow to 100 times its original height?

3. In addition to four dogs, Eldon has four children. The youngest, Betty, is nine years old; then there are twin boys, Arthur and Robert; and finally there's Laura, the eldest, whose age is equal to the combined ages of Betty and Arthur. Also, the combined ages of the twins are the same as the combined ages of the youngest and the eldest. How old is each child? (DISCOVER Magazine)

Solution :

1. This problem is best solved by working it backward. How many biscuits did the fourth dog find? Well, dividing that number by 2 and subtracting 1, we get 0. Reversing the procedure, adding 1 to 0 and then multiplying by 2, we get 2. Thus the last dog found 2 biscuits. Adding 1 and multiplying by 2, we get 6, the number of biscuits found by the third dog. Adding 1 and multiplying by 2, we get 14, the number found by the second dog. Finally, adding 1 and multiplying by 2, we get 30, the number of biscuits originally in the bowl.

2. The plant was initially, say, 1unit tall (the length of a unit really doesn't matter). After one day the plant was 1½  units tall. The next day it gained 1/3 of 1½, which is ½ , so it was then 2 units tall. The day after that, it gained ¼ of 2, which is again ½. So the plant actually gained ½ unit each day. After 198 days it gained 99 units, and it was then 100 times its height on the first day. Thus the answer is 198 days.

3. Let x be the age of each twin and y be the age of Laura. Then y = x+ 9 and y + 9 = 2x. This makes x = 18 and y = 27. Thus the twins are 18 and Laura 27.

Puzzle (4):

AL THE CHEMIST (by RAYMOND SMULLYAN)

1. The Chemist - not an Alchemist, though his name might suggest it - one day partially filled a container with some concoction or other. He knew the volume of fluid in the container, as well as the volume of empty space, and realized that two-thirds of the former was equal to four-fifths of the latter. Was the container then less than half full, more than half full, or exactly half full?

2. On another occasion, Al made a mixture of water and wine. There was more water than wine - in fact, the excess of water over wine was equal to one-fourth the quantity of wine. Al then added 12 ounces of wine, at which point there was one ounce more of wine than water.

According to another version of the story, before Al added the 12 ounces of wine, he first boiled off 12 ounces of water (the net effect being that he replaced 12 ounces of water with wine), and again there was one more ounce of wine than water.

Would there be more mixture present at the end of the first version or the second?

Solution :

1. Let x be the amount of fluid in the container and y be the amount the container would hold if full. The volume of empty space is then y-x, so 2/3x = 4/5(y-x). This makes x = 6/11y, so the container is 6/11 full, which is more than half.

2. Since fluid was added in the first version but not in the second (in which 12 ounces of water was merely replaced by 12 ounces of wine), it might be tempting to conclude that the quantity of fluid at the end of the first version would be greater than at the end of the second, but this would be wrong, as we will now see.

For the first version, let x be the amount of wine initially present and y the amount of water.Then the excess of water over wine is y-x. Thus y-x = 1/4x, which makes y = 5/4x. After adding 12 ounces of wine, there is then one more ounce of wine than water, so x+12 = y +1, and so y = x+11. And since y = 5/4x, we get x = 44 and y = 55. Thus, according to this version, there was initially 99 ounces of mixture and later, 111ounces.

For the second version, we still have the first equation y-x = ¼ x, but the second equation is now x+12 = (y-12) + 1. This makes x = 92 and y = 115. Thus 207 ounces of mixture remained at the end of the second version, which is more than the 111 ounces of the first version.

Puzzle (5):

ESCAPE FROM TARANTULA NEBULA (by CLIFFORD A. PICKOVER)

The Tarantula nebula, a mix of gaz and dust in the large magellanic cloud, one of the Milky Way's two company galaxies, is a nice place to visit - if the inhabitants are not around. One day while exploring the nebula, you are abducted by the mathematical Tarantulans. If you ever wants to return to Earth, they tell you, you must pass a test They take you to a chamber floating in space, made of rooms connected by holes in the walls.

You start at IN, fly through the holes, and finally leave at OUT. Each time you fly through a hole, you add the number next to the hole to your cumulative sum. To leave at OUT you must have flown through every room at least once and have achieved a sum of exactly 30.

The Tarantulans want to make your life hell! In the back room lurks a Tarantulan guard who makes sure you can never enter his room through the "2" orifice.

To make matters worse, the diabolical Tarantulans have rigged the orifices so that each one you pass through closes behind you, never to open again.

Think quick! You have only one minute to escape or the guard will devour you. (DISCOVER Magazine)

Solution :

Diagrammed here is one solution (5+4+10+2+9), going through only five holes.

Here are several other solutions: (6+10+2+3+4+5), (6+4+3+10+2+5), (9+4+10+2+5), and (5+5+10+2+8).

How many others can you find? What's the largest sum you can create and still escape? (Remember, an orifice closes each time you step through it). How many different ways can you create a given sum? It turns out, for example, that 41 is a special number because there seem to be more than 1000 paths that add up to this sum. On the other hand, there is no way to create a sum of 52, as far as I can tell. Can you find any other "impossible Tarantulan sums?"

Please send your answers to Clifford A. Pickover, c/o DISCOVER, 114 Fifth Ave., New York, N. Y. 10011-5690.

Puzzle (6):

How many acres are in the interior tri­angular lake? (by SAM LOYD)

I went to Lakewood the other day to attend an auction sale of some land, but did not make any purchases on account of a peculiar problem which developed. The land was advertised as shown in the posters on the fence as 560 acres, including a triangular lake. The three plots show the 560 acres without the lake, but since the lake was included in the sale, I, as well as other would-be purchasers, wished to know whether the lake area was really deducted from the land.

The auctioneer guaranteed 560 acres "more or less". This was not satisfactory to the purchasers, so we left him arguing with some katydids, and shouting to the bullfrogs in the lake, which in reality was a swamp.

The question I ask our puzzlists is to determine how many acres there would be in that triangular lake, surrounded as shown by square plots of 370, 116 and 74 acres.

The problem is of peculiar interest to those of a mathematical turn, in that it gives a positive and definite answer to a proposition which, according to usual methods, produces one of those ever-decreasing, but never-ending decimal fractions. (Edited by Martin Gardner)

Solution :

Form a right-angled triangle ABD with sides 9 = 4 + 5 and 17 = 7 + 10. By the Pythagorean theorem, the square of the hypothenuse AB is given by AB² = 9² + 17² = 81 + 289 = 370 - exactly the size in acres of the biggest square in the diagram.

Thinking of D as the origin, find point C with coordinates (7, 4). Let CE 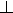 AD, and CF   BD.

In ACE, the Pythagorean theorem gives AC² = 5² + 7² = 25 + 49 = 74 - another square in the diagram.   To get the third square apply the Pythagorean theorem to BFC: BC² = 4² + 10² = 16 + 100 = 116, which proves that ABC is exactly of the shape of the triangular lake. Now then S_(ABC) = S_(ABD) - S_(ACE) - S_(BFC) - S_(CEDF) = 9·17/2 - 5·7/2 - 4·10/2 - 4·7.

We thus obtain S_(ABC) = 76.5 - 17.5 - 20 - 28 = 11.

As Sam Loyd notes: In this remarkable problem we find that the lake contains exactly 11 acres, therefore the approximate answer of "nearly 11 acres" is not sufficiently correct.

Puzzle (7):

How deep is the lake? (by SAM LOYD)

The poet Longfellow was a fine mathematician who often spoke about the advantages of clothing mathematical problems in such attractive garb that they would appeal to the fancy of the student instead of following the dry, technical language of the textbooks.

The water lily problem is one of several introduced in Longfellow's novel, Kavanagh. It is so simple that anyone, even without a knowledge of mathematics or geometry, could solve it, yet it illustrates an important geometrical truth in a never­to-be-forgotten way. I forget the exact language of the problem, as Longfellow described it to me personally during a discussion on the subject, but it concerns a water lily growing in a lake:

The flower was one span above the surface of the water, and when swayed by the breeze would touch the surface at a distance of two cubits, from which data one could compute the depth of the lake.

Now, let us suppose, as shown in the sketch, that the water lily is ten inches above the surface of the water, and that if it were pulled over to one side it would disappear under the surface at a point twenty-one inches from where it originally stood. What is the depth of the water'? (Mathematical Puzzles of Sam Loyd, Edited by Martin Gardner)

Solution :

Euclid says: "When two chords of an are intersect within acircle, the products of the parts of one will be equal to the products of the parts of the other." In the following illustration the surface of the water forms the chord of one are, and since each part of this chord is 21 inches, the product is 441 inches.

The stem of the lily forms the other intersecting chord, and as its height above the water forms one part of the chord, that part, 10 inches, multiplied by the other part, must be the same as the 441 inches obtained by the parts of the other chord. So divide 441 by 10, and we get 44.1 inches as the other part of that chord.

Adding the 10 and the 44.1,we get 54.1 for the total length of the chord from A to F, which is the diameter of the circle.This we must halve to get the radius, 27.05, but as the flower stood ten inches above the surface of the water, we must deduct that ten inches to obtain the depth of the lake - 17.05 inches.

Puzzle (8):

How large was the grindstone when given to the second man? (by SAM LOYD)

It is told that two honest Syrians pooled their savings and bought a grindstone. Because they lived several miles apart, they agreed that the elder man should keep the grindstone until he had reduced it in sire by just one-half, then it should be turned over to the other.

The grindstone was exactly 22 inches in diameter, with a 3 and 1/7 inch hole in the center for the shaft, as shown in the picture. What would be the diameter of the stone when given to the second owner? (Mathematical Puzzles of Sam Loyd, Edited by Martin Gardner)

Solution :

The best method of solving this problem is based on the fact that areas of circles are proportional to the squares of their diameters. If we inscribe a square, ABCD, on a circle the size of the original grindstone, then circle E, inscribed within that square, will have exactly one-half the area of the larger circle.

Half the area of the grindstone's hole must now be added to circle E. To do this we inscribe a square on the hole, and within this square we inscribe a circle. The smaller circle will therefore be half the area of the hole. We place the small circle at G so that its diameter forms the side of a right triangle, the base of which is the diameter of circle E.

The hypotenuse, HI, will then be the diameter of a circle with an area equal to the combined areas of circle E and the small circle at G. This circle, shown with a dotted line, represents the size of the grindstone after half the stone has been used. Its diameter can be calculated as follows:

The diameter of circle E is the same as the side of the largest square. Knowing the diagonal of this square to be 22 inches, we arrive at the square root of 242 for the side of the square and the diameter of circle E. A similar procedure shows the diameter of the smallest circle to be the square root of 242/49.

The square of the diameter of the dotted circle equals the sum of the squares of the two diameters cited above. So we add 242 to 242/49 to obtain 12100/49, the square root of which is 110/7 or 15 and 5/7. This is the diameter in inches of the dotted circle, and the precise answer to the problem. (Mathematical Puzzles of Sam Loyd, Edited by Martin Gardner)

Puzzle (9):

What is the most economical form of a tank designed to hold 1,000 cubic feet? (by SAM LOYD)

HERE is a practical plumbing lesson which will interest those of a mechanical turn of mind. Plumbers, boilermakers and tank builders estimate in cubic feet, reckoning seven and a half' gallons to the cubic foot, which is close enough for all practical purpose. Of course a mathematician would tell us that there are 1,728 cubic inches to a cubic foot, because 12x12x12 = 1,728, while to seven and one-half gallons there are 1,732½, cubic inches, but then plumbers are a liberal set of fellows who cheerfully throw in the extra four and a half inches.

A plumber wanted to estimate the lowest possible cost of a copper tank to hold 1,000 cubic feet. Copper comes in sheets three feet square, worth $1.00 per square foot, so the problem is to determine the most economical dimensions of a rectangular tank capable of holding 1,000 cubic feet. It is self evident that if the bottom of the copper tank is ten feet square, 10 multiplied by 10 gives 100 as the area of the bottom, which multiplied by 10 for the depth, gives the correct dimensions of a tank which will hold 1,000 cubic feet.

A cube ten feet square will hold 1,000 cubic feet it is true, but that would require 500 feet of copper (100 on the bottom and each of the four sides). The point of our problem is to determine the most economical form of a tank that will hold 1,000 cubic feet and use the least possible amount of copper.

It is a simple everyday piece of shop work which any mechanic would tackle in a way satisfactory to himself, but which mathematicians will discover involves the "duplication of the cube." (Mathematical Puzzles of Sam Loyd, Edited by Martin Gardner)

Solution :

In the plumber's problem it will be found that a tank with a square base, twice as wide as it is deep, gives the most economical form. If a cube close to 12.6 feet square holds 2,000 cubic feet, then half that depth would give the required 1,000 cubic feet.

[The exact dimensions of the required tank cannot be stated in rational numbers because they concern one half of a "duplicated cube". Expressed in irrational numbers, the tank would have a length and width equal to the cube root of 2,000, and a depth equal to one-half the cube root of 2,000. M.G.] (Mathematical Puzzles of Sam Loyd, Edited by Martin Gardner)

Puzzle (10):

Will the cat or dog win the race? (by SAM LOYD)

Many years ago, when Barnum's Circus was of a truth "the greatest show on earth," the famous showman got me to prepare for him a series of prize puzzles for advertising purposes. They became widely known as the Questions of the Sphinx, on account of the large prizes offered to any one who could master them.

Barnum was particularly pleased with the problem of the cat and dog race, letting it be known far and wide that on a certain first day of April he would give the answer and award the prizes, or, as he aptly put it, "let the cat out of the bag, for the benefit of those most concerned."

The wording of the puzzle was as follows: "A trained cat and dog run a race, one hundred feet straightaway and return. The dog leaps three feet at each bound and the cat but two, but then she makes three leaps to his two. Now, under those circumstances, what are the possible outcomes of the race?"

The fact that the answer was to be made public on the first of April, and the sly reference to "letting the cat out of the bag," was enough to intimate that the great showman had some funny answer up his sleeve. (Mathematical Puzzles of Sam Loyd, Edited by Martin Gardner)

Solution :

The cat wins, of course. It has to make precisely 100 leaps to complete the distance and return. The dog, on the contrary, is compelled to go 102 feet and back. Its thirty-third leap takes it to the 99-foot mark and so another leap, carrying it two feet beyond the mark, becomes necessary. In all, the dog must make 68 leaps to go the distance. But it jumps only two­thirds as quickly as the cat, so that while the cat is making 100 leaps the dog cannot make quite 67.

But Barnum had an April Fool possibility up his sleeve. Suppose that the cat is named Sir Thomas and the dog is female! The phrase "she makes three leaps to his two" would then mean that the dog would go 9 feet while the cat went 4. Thus when the dog finishes the race in 68 leaps, the cat will have traveled only 90 feet and 8 inches.

[This same puzzle stirred up considerable chagrin in London when Henry Dudeney published it in the April 1, 1900, issue of The Weekly Dispatch. Dudeney's version, a race between a gardener (female) and a cook (male), will be found in his Amusements in Mathematics, problem 428.-M.G.]