|
|
|
|
|
VĂN HỌC |
GIAI THOẠI | TIỂU LUÂN | THƠ | TRUYỆN | THỜI LUẬN | NHÂN VẬT | ÂM NHẠC | HỘI HỌA | KHOA HỌC | GIẢI TRÍ | TIỂU SỬ |
-
Link Tác Phẩm và Tác Giả Tác Phẩm
Tác Giả
Thơ Văn Trần Y. Hoa & Bằng hữu
Thơ Văn Trần Yên Hoà & Bằng hữu
Tạp Chí
PHONG HÓA & NGÀY NAY
(Đại học Hoa Sen)
TỰ LỰC VĂN ĐOÀN, tác phẩm
(Viện Việt Học)
VĂN HỌC
Tạp chí Văn Học
DÒNG VIỆT
Trọn bộ DÒNG VIỆT
(1993-2009)
VĂN (Xuân Canh Thìn)
(vanmagazine)
TIỂU THUYẾT THỨ BẢY
NAM PHONG - TRI TÂN
THANH NGHỊ - NGÀY NAY
VĂN HOÁ NGÀY NAY
TẬP SAN SỬ ĐỊA
THẾ KỶ 21 - BÁCH KHOA
Tạp Chí VHNT Miền Nam
TÂN VĂN
TIN VĂN
Tạp chí ĐỌC VÀ VIẾT
THƯ QUÁN BẢN THẢO
Sách Xưa
• QUỐC VĂN GIÁO KHOA THƯ:
- Lớp Sơ Đẳng
- Lớp Đồng Ấu
- Lớp Dự Bị
• TỦ SÁCH TIẾNG VIỆT
• KHO SÁCH XƯA
• QUÁN VEN ĐƯỜNG
• LITTLE SAIGON
Phim và Hình Ảnh Xưa
- Cuộc Di Cư Năm 1954
- Phim "Chúng Tôi Muốn Sống"
- Phim "Nắng Chiều", 1973
- Phim Chân Trời Tím, 1971
- Hình ảnh xưa
eBooks
-
Giải Đề Thi Toán Quốc Tế môn Hinh Hoc -1 (Học Xá) Ad-23-Index Ad-23-Index = (Ad-23-468x60created-2-1-10) (Học Xá)
24-7-2011 | KHOA HỌC
Giải Đề Thi Toán Quốc Tế (Hình Học) các năm 1965 ... 1997
HỌC XÁ
Share File.php Share File




1965 (IMO 7th) 1975 (IMO 17th) 1985 (IMO 26th) 1987 (IMO 28th) 1997 (IMO 38th)
:: IMO 7th (1965, German)
(http://www.imo-official.org/year_info.aspx?year=1965)
Cho tam giác OAB có góc O nhọn. M là điểm tùy ý trên AB. P và Q là chân đường thẳng góc kẻ từ M đến OA và OB lần lượt. Tìm quĩ tích của H, trực tâm tam giác OPQ. Quĩ tích là gì nếu M thay đổi bên trong OAB?
(Consider
 OAB with acute angle AOB. Through a point M
OAB with acute angle AOB. Through a point M  O perpendiculars are drawn to OA and OB, the feet of which are P and Q respectively. The point of intersection of the altitudes of
O perpendiculars are drawn to OA and OB, the feet of which are P and Q respectively. The point of intersection of the altitudes of  OPQ is H. What is the locus of H if M is permitted to range over (a) the side AB, (b) the interior of
OPQ is H. What is the locus of H if M is permitted to range over (a) the side AB, (b) the interior of  OAB?
OAB?
BÀI GIẢI
 Gọi C và D là chân đường thẳng góc kẻ từ A đến OB và từ B đến OA. Ta thấy rằng trực tâm của tam giác OPQ phải nằm trên DC.
Gọi C và D là chân đường thẳng góc kẻ từ A đến OB và từ B đến OA. Ta thấy rằng trực tâm của tam giác OPQ phải nằm trên DC.
Thật vậy, nếu từ P kẻ một đường cao của
 OPQ, gặp DC tại H, ta sẽ chứng minh đường cao thứ hai kẻ từ Q của
OPQ, gặp DC tại H, ta sẽ chứng minh đường cao thứ hai kẻ từ Q của  OPQ cũng qua H.
OPQ cũng qua H.
Vì MP // BD ==> AM / MB = AP / PD.
Ta cũng có PH // AC ==> AP / PD = CH / HD
và MQ // AC ==> AM / MB = CQ / QB.
So sánh những tỷ lệ trên, ta có CH / HD = CQ / QB. Tỷ lệ này chứng tỏ QH // BD ==> QH OP.
Do đó QH chính là đường cao thứ hai của
 OPQ.
OPQ.
Vậy: Quĩ tích của H, trực tâm
 OPQ, chính là đoạn thẳng DC.
OPQ, chính là đoạn thẳng DC.
Giả thử M nằm trên đường A' B' // AB với A' trên OA và B' trên OB thì quỹ tích của H là đoạn thẳng D'C' // DC. Vậy nếu M di chuyển bên trong
 OAB thì quỹ tích của H là vùng bên trong ODC.
OAB thì quỹ tích của H là vùng bên trong ODC.
Ad-22-A_Newest-Feb25-2022 Ad-22-A_Newest-Feb25-2022
:: IMO 17th (1975, Bulgaria)
(http://www.imo-official.org/year_info.aspx?year=1975)
Ở ngoài tam giác ABC, lập những tam giác ABR, BCP, CAQ sao cho
 CBP =
CBP =  CAQ = 45o,
CAQ = 45o,  BCP =
BCP =  ACQ = 30o,
ACQ = 30o,  ABR =
ABR =  BAR = 15o. Chứng minh rằng
BAR = 15o. Chứng minh rằng  QRP = 90o và QR = RP.
QRP = 90o và QR = RP.
(On the sides of an arbitrary triangle ABC, triangles ABR, BCP, CAQ are constructed externally with
 CBP =
CBP =  CAQ = 45o,
CAQ = 45o,  BCP =
BCP =  ACQ = 30o,
ACQ = 30o,  ABR =
ABR =  BAR = 15o. Prove that
BAR = 15o. Prove that  QRP = 90o and QR = RP).
QRP = 90o and QR = RP).
BÀI GIẢI
 Dựng tam giác đều ABM.
Dựng tam giác đều ABM.
Ta có:
 RAM =
RAM =  RBM = 45o,
RBM = 45o,  AMR =
AMR =  BMR = 30o,
BMR = 30o,  ARM =
ARM =  BRM = 105o.
BRM = 105o. Vậy
 QAC ~
QAC ~  RAM ==> QA / RA = CA / MA
RAM ==> QA / RA = CA / MA ==>
 QRA ~
QRA ~  CMA
CMA ==> QR / CM = RA / MA (1)
và
 QRA =
QRA =  CMA (2).
CMA (2). Tương tự như thế, ta cũng có:
 PBC ~
PBC ~  RBM ==> PB / RB = CB / MB
RBM ==> PB / RB = CB / MB ==>
 PRB ~
PRB ~  CMB
CMB ==> PR / CM = RB / MB (3) và
 PRB =
PRB =  CMB (4)
CMB (4)
Để ý những tỷ số của (1) và (3), vì RA = RB và MA = MB, nên: QR = PR.
Cộng hai vế của (2) và (4) ==>
 QRA +
QRA +  PRB =
PRB =  AMB = 60o.
AMB = 60o. Từ đó suy ra:
 QRP = 90o.
QRP = 90o.
Ad-22-A_Newest-Feb25-2022 Ad-22-A_Newest-Feb25-2022
:: IMO 26th (1985, Finland)
(http://www.imo-official.org/year_info.aspx?year=1985)
1. Một vòng tròn có tâm O trên cạnh AB của một tứ giác nội tiếp ABCD. Ba cạnh kia tiếp xúc với vòng tròn. Chứng minh: AD + BC = AB.
(A circle has center on the side AB of the cyclic quadrilateral ABCD. The other three sides are tangent to the circle. Prove that AD + BC = AB).
BÀI GIẢI
 Ðặt
Ðặt  JCO =
JCO =  và
và  KDO =
KDO = 
==>
 C = 2
C = 2 và
và  D = 2
D = 2
Tứ giác nội tiếp ABCD có các góc đối bù nhau, vậy
 A +
A +  C = 180o
C = 180o
==>
 A + 2
A + 2 = 180o
= 180o
==>
 A = 180o - 2
A = 180o - 2
Chọn điểm M trên AD sao cho AM = AO ta sẽ có
 MAO cân,
MAO cân,
==>
 AMO = (180o-A)/2
AMO = (180o-A)/2
==>
 KMO =(180o-(180o-2
KMO =(180o-(180o-2 ))/2 =
))/2 = .
.
Hai tam giác vuông OKM và OJC có OK = OJ (=R) và
 KMO =
KMO =  JCO (=
JCO (=  ), vậy chúng bằng nhau; suy ra KM = JC (1).
), vậy chúng bằng nhau; suy ra KM = JC (1).
Chọn điểm N trên BC sao cho BN = BO ta sẽ có
 NBO cân. Cũng chứng minh tương tự như trên ta sẽ có
NBO cân. Cũng chứng minh tương tự như trên ta sẽ có  JNO =
JNO =  và hai tam giác vuông OKD , OJN bằng nhau; suy ra KD = JN (2).
và hai tam giác vuông OKD , OJN bằng nhau; suy ra KD = JN (2).
Ta có : AO = AM = AK + KM
BO = BN = BJ + JN
Cộng hai vế và từ (1), (2) ta được: AO + BO = AK + JN + BJ + KM
==> AO + BO = AK + KD + BJ + JC ==> AB = AD + BC
2. Vẽ vòng tròn O đi qua hai đỉnh A, C của tam giác ABC, cắt hai cạnh AB và BC theo thứ tự tại K và N. Các vòng ngoại tiếp hai tam giác ABC và KBN cắt nhau tại B và M. Chứng minh:
 OMB = 90o.
OMB = 90o. (A circle with center O passes through the vertices A and C of triangle ABC and intersects the segments AB and BC again at distinct points K and N, respectively. The circumscribed circles of the triangles ABC and KBN intersect at exactly two distinct points B and M. Prove that angle OMB is a right angle).
BÀI GIẢI
 Phương tích của điểm I đối với vòng tròn tâm O, bán kính r là đại lượng d2- r2 trong đó d là khoảng cách IO: d2- r2 = IO2 - ON2 = IC . IA = IN . IK
Phương tích của điểm I đối với vòng tròn tâm O, bán kính r là đại lượng d2- r2 trong đó d là khoảng cách IO: d2- r2 = IO2 - ON2 = IC . IA = IN . IK
Trục đẳng phương (ace radical) của hai vòng tròn là quỹ tích các điểm có phương tích bằng nhau đối với hai vòng tròn đó.
Nếu hai vòng tròn cắt nhau tại hai điểm thì trục đẳng phương đi qua hai điểm ấy.
Trường hợp trong bài: AC, KN, BM lần lượt là trục đẳng phương của từng cặp vòng tròn O&O1, O&O2, O1&O2. Ba trục trên đồng qui tại I (tâm đẳng phương).
Do vậy ta có đẳng thức: IM . IB = IN . IK = IO2 - ON2 (1)
Vì
 NMI =
NMI =  NCA (cùng bù với
NCA (cùng bù với  AKN), vậy
AKN), vậy  NMI +
NMI +  NCI = 180o. Do đó tứ giác IMNC nội tiếp, cho ta đẳng thức: BM.BI = BN.BC =
BO2 - ON2 (2)
NCI = 180o. Do đó tứ giác IMNC nội tiếp, cho ta đẳng thức: BM.BI = BN.BC =
BO2 - ON2 (2)
Trừ (1) và (2), ta được: IM.IB - BM.BI = IO2 - BO2
IB (IM - BM) = IO2 - BO2
(IM + BM) (IM - BM) = IO2 - BO2
IM2 - BM2 = IO2 - BO2 ==> OM
 IB
IB
Ad-22-A_Newest-Feb25-2022 Ad-22-A_Newest-Feb25-2022
:: IMO 28th (1987, Cuba)
(http://www.imo-official.org/year_info.aspx?year=1987)
Tam giác ABC có 3 góc nhọn. Ðường phân giác của góc A cắt BC tại L và vòng tròn ngoại tiếp tại N. Từ L hạ hai đường thẳng góc xuống AB và AC theo thứ tự là LK và LM. Chứng minh diện tích tứ giác AKNM = diện tích tam giác ABC.
(In an acute-angled triangle ABC the interior bisector of the angle A intersects BC at L and intersects the circumcircle of ABC again at N. From point L perpendiculars are drawn to AB and AC, the feet of these perpendiculars being K and M respectively. Prove that the quadrilateral AKNM and the triangle ABC have equal areas).
BÀI GIẢI
 S(ABC) = 1/2 AB.AC.sinA (a)
S(ABC) = 1/2 AB.AC.sinA (a)
S(AKNM) = 1/2 AN.KM (b)
Theo định lý hàm số sin trong
 AKM ta có:
AKM ta có:
KM/sinA = AL ==> AL.sinA = KM (1)
Hai tam giác ABL và ANC đồng dạng vì:
 BAL =
BAL =  NAC và
NAC và  ABL =
ABL =  ANC cho ta hệ thức:
ANC cho ta hệ thức:
AB / AN = AL / AC ==> AB.AC = AN.AL (2)
Từ (2) ta có thể biến đổi (a) thành:
S(ABC) = 1/2 AN.AL.sinA
Thay (1) vào hệ thức trên ta được: S(ABC) = 1/2 AN.KM.
Ðó chính là S(AKNM) ở (b). Vậy: S(ABC) = S(AKNM)
Ad-22-A_Newest-Feb25-2022 Ad-22-A_Newest-Feb25-2022
:: IMO 38th (1997, Argentina)
(http://www.imo-official.org/year_info.aspx?year=1997)
Tam giác ABC có góc A nhỏ nhất. Hai điểm B và C chia vòng tròn ngoại tiếp thành hai cung. Ðiểm U trên cung BC không chứa A. Trung trực của AB và AC cắt AU lần lượt tại V và W. BV cắt CW tại T. Chứng minh: AU = TB + TC.
(The angle at A is the smallest angle of triangle ABC. The points B and C divide the circumcircle of the triangle into two arcs. Let U be an interior point of the arc between B and C which does not contain A. The perpendicular bisectors of AB and AC meet the line AU at V and W, respectively. The lines BV and CW meet at T. Show that AU = TB + TC).
BÀI GIẢI
 Kéo dài BV và CW gặp vòng tròn ngoại tiếp tam giác ABC tại X và Y.
Kéo dài BV và CW gặp vòng tròn ngoại tiếp tam giác ABC tại X và Y. Vì JW là đường trung trực của AC (theo giả thiết) nên
 AWC cân ==>
AWC cân ==>  CAU =
CAU =  ACY, ta cũng có
ACY, ta cũng có  AYC =
AYC =  CUA (cùng chắn cung AC), cạnh AC chung, vậy hai tam giác ACY và CAU bằng nhau; suy ra: AU = CY ==> AU = CY = TY + TC (1)
CUA (cùng chắn cung AC), cạnh AC chung, vậy hai tam giác ACY và CAU bằng nhau; suy ra: AU = CY ==> AU = CY = TY + TC (1)
Vì IV là đường trung trực của AB (theo giả thiết) nên
 AVB cân ==>
AVB cân ==>  BAU =
BAU =  ABX, ta cũng có
ABX, ta cũng có  CAU =
CAU =  ACY =
ACY =  ABY, vậy
ABY, vậy  BAU +
BAU +  CAU =
CAU =  ABX +
ABX +  ABY ==>
ABY ==> 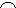 BC =
BC = 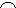 YX ==>
YX ==>  BYC =
BYC =  YBX ==>
YBX ==>  YTB cân ==> TY = TB (2)
YTB cân ==> TY = TB (2)
Thế (2) vào (1) ta được: AU = TB + TC
Ad-22-A_Newest-Feb25-2022 Ad-22-A_Newest-Feb25-2022
-
Bài Khảo Cứu & Bài Tập Hình Học (Học Xá) • Bài Khảo Cứu
Cùng Mục (Link) • Có Và Không Của Thế Gian (Hoàng Dung)
• DNA, Đặc Tính Sự Sống và Sinh Vật (Hoàng Dung)
• Thử Tìm Hiểu ChatGPT (Đào Như)
• Những khám phá mới về Chất Trắng Trong Não Bộ (Trần Hồng Văn)
• Siêu Thượng Không Gian: Chương Kết Luận (Trà Nguyễn)
• Vài Mạn Đàm Về Sao Trời (Hoàng Dung)
• Vật Lý Lượng Tử Và Ý Nghĩa Thiền Học Của Vật Chất (Hoàng Dung)
• Những Quan Niệm và Học Thuyết Mới về Vũ Trụ (Phần 2) (Trần Hồng Văn)
• Những Quan Niệm và Học Thuyết Mới về Vũ Trụ (Phần 1) (Trần Hồng Văn)
• “Mỹ Ngữ” Và “Anh Ngữ” Khác Nhau Thế Nào? (Đàm Trung Pháp)

• Hình Học (Bài Tập)
Bài 48 (Điểm Schiffler của tam giác)
Bài IOM: 7 - 38, 41 - 45, 46 - 51
• Anh Ngữ
• Đố Vui: 1, 2
Liên Kết Trong Mục Học Toán (Học Xá) Liên Kết
IMO
Wolfram MathWorld
The Math Forum
USAmts
Komal
MathLinks
Cut-The-Knot
Từ Điển Anh Việt
|
© Hoc Xá 2002 (T.V. Phê - phevtran@gmail.com) |

















